建青实验第一学期初三数学期中考试题
（满分150分，考试时间100分钟） 出卷人：初二备课组 审卷人：初二备课组
所有答案均写在答卷纸上，不然不能分！
1、选择题（本大题6小题，每题4分，共24分）
1．下列函数中是二次函数的是 （ ）
（A）
（B）
（C）
（D）
2．二次函数
的图象与轴的交点的个数是 （ ）
（A）0 （B）1 （C）2 （D）3
3．在△ABC中，点D、E分别在AB、AC 边上，∠B=∠AED，则下列结论中不正确的是 （ )
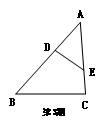（A）AD ：AC=AE ：AB； （B）AD·AB=AE·AC；
（C）DE ：BC=AD ：AC； DE ：BC=AD ：AB．
4．下列说法中，错误的是 （ ）
（A）长度为1的向量叫做单位向量；
（B）假如
，且
，那样
的方向与
的方向相同；
（C）假如
或
，那样；
（D）假如
，
，其中
是非零向量，那样。
5．下列四个命题中，真命题是 （ ）．
（A）直角三角形都相似 （B）相似三角形角平分线的比等于相似比
（C）等腰三角形都相似 （D）相似三角形面积的比等于相似比的平方
6．假如点D、E分别在ΔABC的边AB、AC上，下列条件中 可以 推出DE∥BC的是 （ ）
AB= 3，BC= 3； （B） BD= 3，AE= 3；
（C） AD= 2，AE= 2； AD=
，EC= ．
2、填空题：（每题4分，共48分）
7．线段a、b、c、d是成比率的四条线段，其中a=2，b=3，c=4，那样线段d的长可以是___________；
8．若
，则
9．在比率尺为1：
10000的地图上，相距4厘米的两地A、B的实质距离为__________米．
10．已知线段AB的长为10厘米，点P是线段AB的黄金分割点，那样 较 短 的线段AP的长等于__________厘米。
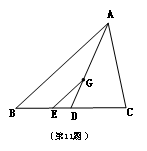
11．如图，点G是
的重点，联结AG并延长交BC于点D，GE
AB交BC于点E，若AB=12，那样GE=___________。
（第13题）
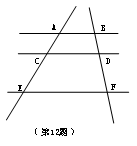
12．如图，ABCDEF，假如AC=2，AE=5.5，DF=3，那样BD=___________。
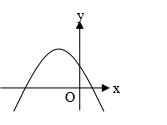
13．抛物线
如图所示，用或或号连接
______0， ______0， 
______0， 
______0。
14．二次函数
向右平移4个单位，向下平移2个单位后可得抛物线__________。
15．二次函数
的图像的最高点坐标是__________。
16．二次函数
的图像上有两个点（3，）、（
），那样________ 
（填“”、“”或“”）
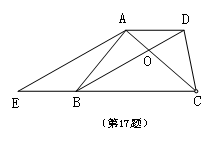17.如图，在梯形ABCD中，ADBC，AC与BD交于点O，DO：BO=1:2，点E在CB的延长线上，假如
=1:3，那样BC：BE=_______。
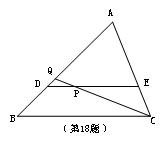
18．如图，DEBC，且过的重点，分别与AB、AC交于点D、E，点P是线段DE上
一点，CP的延长线交AB于点Q。假如
，那样的值是_______。
3、 解答卷（本大题共7题，满分78分）
19．（本题满分10分）如图，在中，D是AB的中点，联结CD。
（1）若AB=12且
，求AC的长；
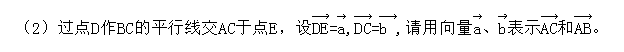
（直接写出结果）
20．（本题满分10分）
已知抛物线
经过点B（-1,0）和点C（2,3）。
（1）求此抛物线的表达式；
（2）假如此抛物线上下平移后过点（-2，-1），试确定平移的方向和平移的距离。
21．（本题满分10分）
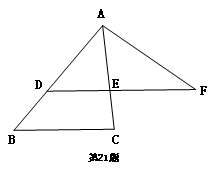如图，在中，点D是AB边上一点，过点D作 DEBC，交AC于点E，点F是DE延长线上一点，联结AF。
（1）假如
，DE=6，求边BC的长；
（2）假如，
，
求的长。
22．（本大题满分10分）
如图，、均为等边三角形，D、E分别在边AB、BC上，G、H在AC边上，写出所有与
一样的三角形，并对其中一个加以证明。
23. （本大题满分12分）
如图，正方形ABCD中，P是CB延长线上一点，DP交AB于N，交AC于M，
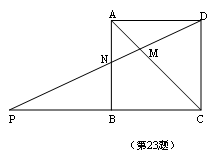（1）求证：
；
（2）假如，求DM的长。
24．（本题满分12分）
如图，已知在平面直角坐标系中，点A（4,0）是抛物线
上的一点，将此抛物线向下平移6个单位后经过点B（0,2），平移后所得的新抛物线的顶点记为C，
新抛物线的对称轴与线段AB的交点记为P。
（1）求平移后所得到的新抛物线的表达式，并写出点C的坐标；
（2）假如点Q是抛物线对称轴上的一点，且
与
相似，求点Q的坐标。
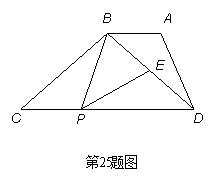
25．（本题满分14分）
如图，在梯形ABCD中，AB∥CD, CD=6，BC=4，∠ABD =∠C，P是CD上的一个动点
，且满足条件：∠BPE =∠C, PE交BD于点E。
求证：△BCP∽△PDE；
（2）假如CP= x , BE=y，求y与x之间的函数关系式；
（3）P点在运动过程中，△BPE能否成为等腰三角形？若能，求 x的值；若否，说明理由。
建青实验2017学年度第一学期初三数学期中考试试题答案
1、C C D B D C
2、7. 6； 8. ； 9.400 ； 10. 
；
11. 4 ； 12. ； 13. 、、、； 14. 
； 15. ；
16. ； 17. ； 18. 
。
19. 解：（1）
D是AB的中点，且AB=12，
AD=， …………………………1分
在
与中，
∽ …………………………2分
…………………………2分
=72…………………………1分
AC=
；…………………………1分
（2）要作图；
； 
。…………………………3分
20. 解：（1）将点B（-1,0）、C（2,3）代入，
得：，………2分 解得： ……………4分
此抛物线的表达式为. ……………1分
（2）在中，当
时，，…………1分
若点（-2，-5）平移后的对应点为（-2，-1），则需将抛物线向上平移4个单位。
（办法不唯一，其他办法酌情给分） ………………2分
21解：DE//BC,
, ……………2分
DE=6, BC=9；……………2分
（2） DE//BC, ……………1分
，
……………1分
∽
……………2分
FA=6，FE=4，
DF=9。……………2分
22. 解：与一样的三角形有：AGD、FGH、CEH；…………3分
（2）选证：与相似。 ……………1分
、均为等边三角形，
，……………1分
，即：
……………2分
在与中，
……………2分
∽ ……………1分
23. 证明：四边形ABCD是正方形
AB//CD，即BN//CD，且AB=CD …………………………2分
…………………………2分
…………………………1分
AB=CD
…………………………1分
（2）解：设DM=
MN=1, PN=3, …………………………1分
AB//CD
AN//CD且BN//CD…………………………1分
…………………………1分
且 …………………………1分
=1 …………………………1分
解得：
DM=2 …………………………1分
24.（1）由题意原抛物线经过点A（4,0），B（0,8） ……………1分
代入得：
解得： ………………………2分
原抛物线表达式： ………………………1分
平移后的抛物线表达式： ………………………1分
点C（1,3） ………………………1分
（2）设直线AB的分析式为：
过点A（4,0）和点B（0,2）
………………………1分
抛物线的对称轴与线段AB交于点P
P（） ………………………1分
由题意的
与相似有两种可能：
1°，得CQ=4；点Q（1，-1） ………………………2分
2°，得CQ=； 点Q（1，
）………………………2分
25. 证明: AB∥DC，∠ABD=∠BDC ………………………1分
∠ABD =∠C，∠BDC =∠C ……………………………1分
∠BPD =∠BPE+∠EPD
∠BPD =∠PBC+∠C
又∠BPE =∠C
∠PBC =∠EPD ……………………………………1分
△BCP∽△PDE …………………………………………1分
△BCP∽△PDE
, ……………………………………………………1分
CP= x , BE=y，BD=BC=4,CD=6
DP= 6 - x , DE= 4 – y
, …………………………………………………1分
（0
能。 ………………………1分
若BP=PE，则△BCP≌△PDE，
PD=BC=4, x=2 ……………………………………………2分
若BE=PE，则∠BPE=∠PBE=∠C=∠CDB，
△BEP∽△CBD，PE：PB=BC：CD=2：3
又PD：BC=PE：PB
即（6-x）：4=2：3，
x= ……………………………………………………2分
若BP=BE，则∠BPE=∠PEB>∠CDB，矛盾. ……………………1分
当x=2或时，△BPE为等腰三角形.
